Stereographic projection
There are several conventions:
First approach
If we use a sphere of radius 1 and project from the north pole $N=(0,0,1)$ to the plane $z=0$ the formulas of stereographic projection and its inverse are
$$ \begin{aligned} (\xi, \eta) &=\left(\frac{x}{1-z}, \frac{y}{1-z}\right) \\ (x, y, z) &=\left(\frac{2 \xi}{1+\xi^{2}+\eta^{2}}, \frac{2 \eta}{1+\xi^{2}+\eta^{2}}, \frac{-1+\xi^{2}+\eta^{2}}{1+\xi^{2}+\eta^{2}}\right) \end{aligned} $$where $(\xi,\eta)$ are coordinates in the plane and $(x,y,z)$ coordinates in $\mathbb{R}^3$
The sphere has a Riemannian metric inherited by the usual metric of $\mathbb{R}^3$, which is translated to the plane $z=0$ as
$$ \left( \begin{array}{cc} \frac{4}{(1+\xi^2+\eta^2)^2} & 0\\ 0 & \frac{4}{(1+\xi^2+\eta^2)^2} \end{array} \right) $$This metric is conformal to the Euclidean metric, so stereographic projection provide isothermal coordinates for the sphere.
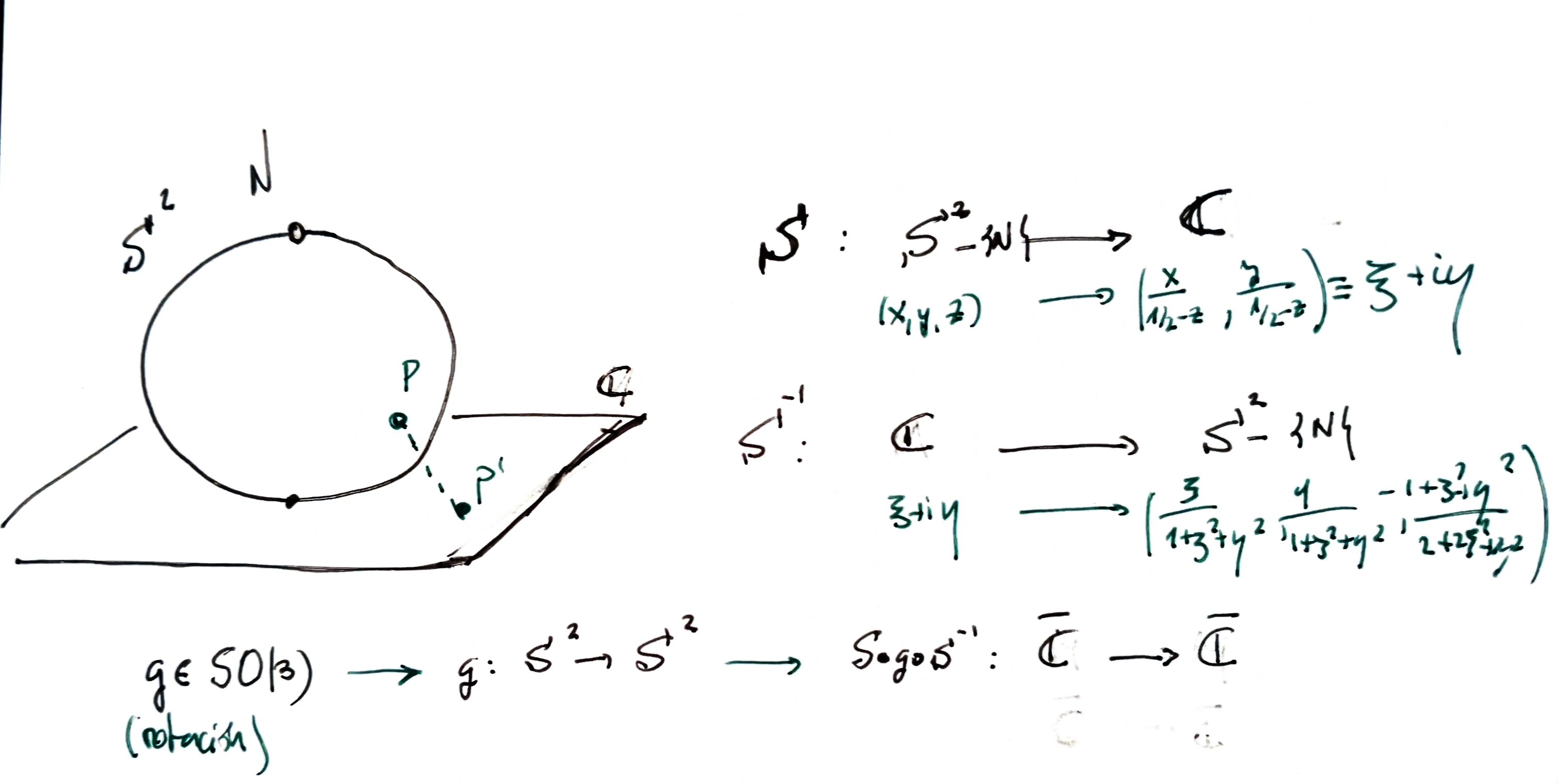
Second approach
If we use a sphere of radius 1/2 and the plane _z_ = −1/2 we have the formulas
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: